레드블랙 트리(Red-Black Tree)
이진 검색 트리로 균형을 이루도록 고안된 검색 트리 구조 중 하나이다.
(높이를 최소한으로 하기에 O(lgn)시간에 수행하도록 보장함)
각 노드당 한 비트의 추가 기억 공간을 가진다. (Red or Black)
노드의 색깔을 제한함으로서 경로가 다른 것보다 두 배 이상 길지 않음을 보장한다.(근사적 균형을 이룬 트리)
- color
- key
- left, right, p
...
레드블랙 특성(Red-Black Property)
1. 모든 노드는 적색이거나 흑색이다.
2. 루트는 흑색이다.
3. 모든 리프(nullptr)는 흑색이다.
4. 노드가 적색이면 그노드의 자식은 모두 흑색이다.
5. 각 노드로부터 그 노드의 자손인 리프로 가는 경로들은 모두 같은 수의 흑색 노드를 포함한다.
레드블랙 트리는 리프를 하나의 경계노드(sentinel)을 사용해서 표현함
(하나의 경계 노드 T.nullptr을 생성하고 모든 리프와 루트의 부모를 표현하도록 함,
경계 노드의 필드 p, left, right, key 등이 프로시저 수행과정에서 채워질 수 있으나 이는 의미를 가지지 않음)
흑색 높이(Black Height)
한 노드 x에서 리프까지의 경로에 있는 모든 흑색 노드의 개수; bh(x) -> 레드블랙 트리는 최대 2lg(n+1)의 높이를 가짐
Search, Minimm, Maximum, Sucessor, Predecessor 연산이 O(lgn)의 시간을 소모한다.
Insert, Delete 연산은 레드블랙 특성을 위반할 수 있다.
따라서 특성을 복구해주기 위해서 일부 노드의 색깔과 포인터를 변경해 주어야 한다.
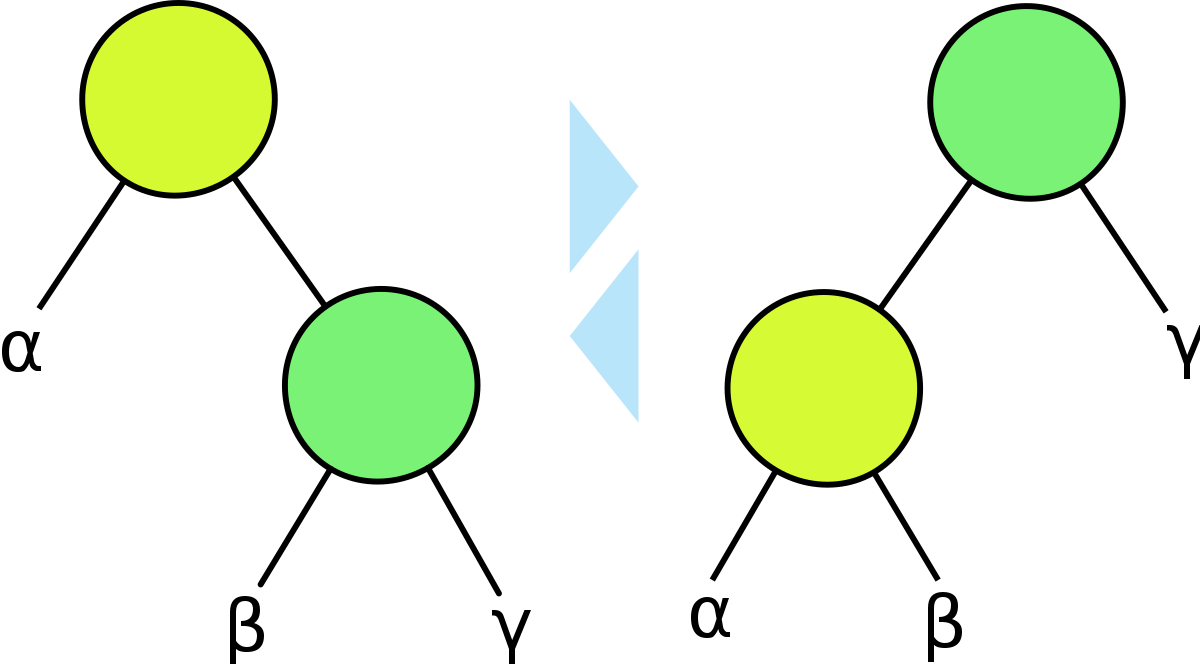
Rotation
- LeftRotation
- RightRotation
Insert
이진 트리처럼 Insert를 수행하되, z를 적색으로 칠한다.
InsertFixup
Insert 과정에서 특성 2, 특성 4가 위반될 수 있다.
z가 루트일 경우 특성 2 위반
z->p가 적색일 때 특성 4 위반
Transplant
Delete
DeleteFixup
#include <iostream>
#define BLACK true
#define RED false
using namespace std;
template <typename T>
struct Node{
T key;
// black: 1, red: 0
bool color;
Node<T> *p, *left, *right;
Node(int _key): key(_key) {}
Node(int _key, bool _color): key(_key), color(_color) {}
};
template <typename T>
class RBTree{
public:
RBTree(void){
nil=new Node<T>(-1);
}
Node<T>* Minimum(Node<T>* x){
while(x->left!=this->nil) x=x->left;
return x;
}
void LeftRotate(Node<T>* x){
Node<T>* y=x->right;
x->right=y->left;
if(y->left==this->nil) y->left->p=x;
y->p=x->p;
if(x->p==this->nil) this->root=y;
else if(x==x->p->left) x->p->left=y;
else x->p->right=y;
y->left=x;
x->p=y;
}
void RightRotate(Node<T>* y){
Node<T>* x=y->left;
y->left=x->right;
if(x->right==this->nil) x->right->p=y;
x->p=y->p;
if(y->p==this->nil) this->root=x;
else if(y==y->p->right) y->p->right=x;
else y->p->left=x;
x->right=y;
y->p=x;
}
void RBInsertFixup(Node<T>* z){
Node<T>* y;
while(z->p->color==RED){
if(z->p==z->p->p->left){
y=z->p->p->right;
if(y->color==RED){
z->p->color=BLACK;
y->color=BLACK;
z->p->p->color=RED;
z=z->p->p;
} else if(z==z->p->right){
z=z->p;
LeftRotate(z);
} else {
z->p->color=BLACK;
z->p->p->color=RED;
RightRotate(z->p->p);
}
} else {
y=z->p->p->left;
if(y->color==RED){
y->p->color=BLACK;
y->color=BLACK;
z->p->p->color=RED;
z=z->p->p;
} else if(z==z->p->left){
z=z->p;
RightRotate(z);
} else {
z->p->color=BLACK;
z->p->p->color=RED;
LeftRotate(z->p->p);
}
}
}
this->root->color=BLACK;
}
void Insert(int key){
Node<T>* z=new Node<T>(key, RED);
Node<T> *x, *y;
x=this->nil; y=this->root;
while(x!=this->nil){
y=x;
if(z->key<x->key) x=x->left;
else x=x->right;
}
z->p=y;
if(y==this->nil) this->root=z;
else if(z->key<y->key) y->left=z;
else y->right=z;
z->left=this->nil;
z->right=this->nil;
RBInsertFixup(z);
}
void Transplant(Node<T>* u, Node<T>* v){
if(u->p==this->nil) this->root=v;
else if(u==u->p->left) u->p->left=v;
else u->p->right=v;
v->p=u->p;
}
void DeleteFixup(Node<T>* x){
Node<T>* w;
while(x!=this->root && x->color==BLACK){
if(x==x->p->left){
w=x->p->right;
if(w->color==RED){
w->color=BLACK;
x->p->color=RED;
LeftRotate(x->p);
w=x->p->right;
}
if(w->left->color==BLACK && w->right->color==BLACK){
w->color=RED;
x=x->p;
} else if(w->right->color==BLACK){
w->left->color=BLACK;
w->color=RED;
RightRotate(w);
w=x->p->right;
} else {
w->color=x->p->color;
x->p->color=BLACK;
w->right->color=BLACK;
LeftRotate(x->p);
x=this->root;
}
} else {
w=x->p->left;
if(w->color==RED){
w->color=BLACK;
x->p->color=RED;
RightRotate(x->p);
w=x->p->left;
}
if(w->right->color==BLACK && w->left->color==BLACK){
w->color=RED;
x=x->p;
} else if(w->left->color==BLACK){
w->right->color=BLACK;
w->color=RED;
LeftRotate(w);
w=x->p->left;
} else {
w->color=x->p->color;
x->p->color=BLACK;
w->left->color=BLACK;
RightRotate(x->p);
x=this->root;
}
}
}
x->color=BLACK;
}
void Delete(Node<T>* z){
Node<T>* x;
Node<T>* y=z;
bool y_original_color=y->color;
if(z->left==this->nil){
x=z->right;
Transplant(z, z->right);
} else if(z->right==this->nil){
x=z->left;
Transplant(z, z->left);
} else {
y=Minimum(z->right);
y_original_color=y->color;
x=y->right;
if(y->p==z) x->p=y;
else{
Transplant(y, y->right);
y->right=z->right;
y->right->p=y;
}
Transplant(z, y);
y->left=z->lef;
y->left->p=y;
y->color=z->color;
}
if(y_original_color==BLACK) DeleteFixup(x);
delete z;
}
private:
Node<T> *root, *nil;
};
AVL Tree
높이 균형을 이룬 이진 검색 트리
각각의 노드 x에 x.h 필드가 존재한다. 각각의 노드 x에 대해 왼쪽과 오른쪽 서브 트리의 높이가 최대 1만큼 차이가 난다.
삽입 연산 이후, | x.right.h - x.left.h | <=2 인 경우, Balance(x) 연산을 수행
Treap(트립)
임의로 만들어진 이진트리는 균형을 이루는 경향이 있기에
만일 항목을 임의로 섞을 경우 삽입할 경우 심하게 불균형을 이뤄 성장할 확률은 낮다.
트립은 항목이 하나씩 주어지는 경우, 임의로 섞은 것처럼 임의로 만들어진 이진 검색 트리를 만들기 위한 방법이다.
노드에 대해 x.key와 추가로 x.priority(우선순위)를 할당한다.
key는 이진 검색 트리의 특성을 따르고, priority는 최소 힙 특성을 따르도록 순서를 정한다.
if v is u's left child → v.key<u.key
if v is u's right child → v.key>u.key
if v is u's child → v.priority>u.priority
키와 우선순위를 각각 가지는 서로 다른 노드가 주어졌을 때, 노드에 대한 트립은 유일하다.
구간 트리
각 노드는 x.int를 포함한다.
IntervalInsert(T, x)
IntervalDelete(T, x)
IntervalSearch(T, i): 구간 i와 겹치는 x.int를 가지는 원소 x가 있는 경우 이에 대한 포인터를 리턴
struct interval{
int low, high;
};
struct Node{
int max;
interval inter;
};